TILING THE DODECAHEDRON
by Leonard Gordon
Word Ways, 1998
Making the Alphabet Dance describes on page 214 lettering the 20 vertices of a dodecahedron with 20 different letters so that the five letters surrounding each of the 12 faces can be anagrammed into a word. This comes from an article entitled "Platonic Relationships" in the February 1980 Word Ways. Upon seeing the book, two questions occurred to me. Can I solve this problem with a computer? Are there solutions that do not use the unabridged dictionaries? The answers to both turned out to be yes. The computer program was neither simple nor speedy, but it found plenty of solutions in smaller dictionaries.
Figure 1 is a Schlegel diagram of the dodecahedron. Schlegel diagrams are possible for all the platonic solids and are normally used in this kind of discussion. The circles number the nodes. Eleven of the pentagon faces are numbered. The five outside nodes define the 12th face.
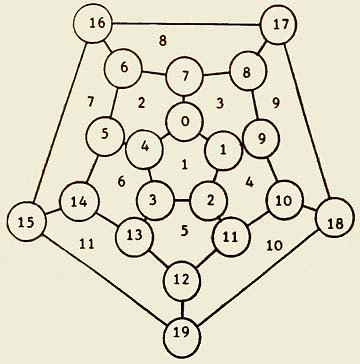
Figure 1
Below are nine solutions (in columns). The numbers to the left in the first table correspond to the 12 pentagon faces in Figure 1; the numbers to the left in the second table correspond to the 20 nodes.
1 black crabs baths gambs botch botch becks bunch birch 2 jambs chalk blank batch knobs knobs blend bumfs blips 3 cramp thraw whack clamp comps holms helms flung smith 4 chirk brown threw mewls mulch thump psych night thraw 5 whelk numbs strum grows thirl crypt prick ketch wreck 6 bowls micks limbs brugh brant brick brank bocks block 7 judos kylix lying dhuti knave inked gonad myops pylon 8 jumpy ethyl conky typic pesky ashen mould flamy spumy 9 gripy towed cowed kelpy dumpy haulm mushy grail gamut 10 neigh pound drupe woken guild gulpy tipsy tried waged 11 owned mixup guimp round virga ridgy tragi poked kendo 12 dungy pyxed podgy dinky gyved glade gusto pardy dungy
0 a a a a o o e u i 1 c r h m c h s n h 2 k b t s h t c h r 3 l s s g t c k c c 4 b c b b b b b b b 5 s k l h n k n s l 6 j l n t k n d m p 7 m h k c s s l f s 8 p t c p p h m l m 9 r w w l m m h g t 10 i o e e u u y i a 11 h n r w l p p t w 12 e u u o i y i e e 13 w m m r r r r k k 14 o i i u a i a o o 15 d x g d v d g p n 16 u y y i e e o y y 17 y e o y y a u a u 18 g d d k d l s r g 19 n p p n g g t d d
The difficulty in this problem was in deciding how the computer should proceed. A human solver can choose a starter word and then continue in any and all directions. The computer must be given explicit instructions. I chose to search in the numerical order of Figure 1 and allow vowels in nodes 0, 10, 12, 14, 16 and 17. The plan is symmetric so exchange between words 2 and 3 was prohibited.
The database for this study was precisely that developed for my Jotto study (see February 1997 Word Ways). Words were classified according to quality and only words from the Official Scrabble Players Dictionary, Chambers Twentieth Century Dictionary or the Merriam-Webster 10th Collegiate were used. Three data banks were established and used appropriately: (1) words with only the chosen starter vowel, (2) words with any one vowel except the starter, and (3) words with two vowels excluding the starter. Working lists came to about 2800 words depending on which vowel was the starter.
The program was very slow-running, so I only found about 100 solutions. A few thousand probably exist. With this database, it is not possible to use Y as the starter vowel. In regard to the consonants, the above examples show the use of J, V and X, although they do not occur often. I did not find any words with Z or Q but this should be possible with words from Webster's Second Unabridged.